The sigmoid function frequently appears in machine learning contexts. It has a simple form: $$
\sigma(x)=\frac{1}{1+e^{-x}}
$$. A naive implementation in C would be:

double sigma(double x)
{
    return 1.0/(1.0+exp(-x));
}

It looks good, right? No, it is not. When $x << 0$, say $x=1000$, exp(-x) will yield NaN, even though $\sigma(x)$ approaches $0$. We need a way to bypass the NaN. Let’s look at the graph of $\sigma(x)$.

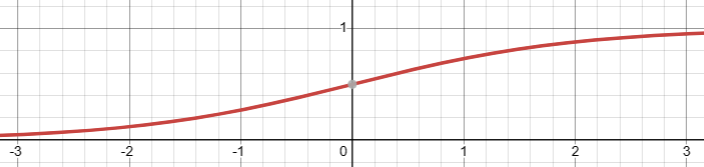
It looks symmetric about $(0, \frac{1}{2})$. If it is the case, $$\begin{equation}
\sigma(x)=1-\sigma(-x)
\end{equation}$$ will have to hold. Let’s try to prove it.

$$\begin{align}
1-\sigma(-x) &= 1-\frac{1}{1+e^x} \\
&=\frac{1+e^x}{1+e^x}-\frac{1}{1+e^x} \\
&=\frac{1+e^x-1}{1+e^x} \\
&=\frac{e^x}{1+e^x} \\
&=\frac{1}{\frac{1}{e^x}+\frac{e^x}{e^x}} \\
&=\frac{1}{e^{-x}+1} \\
&=\sigma(x)
\end{align}$$

Done. It’s proven. Now, whenever $x<0$, we can switch $\sigma(x)$ to $1-\sigma(-x)$, which yields the same value and completely avoids the NaN problem. The following is the code.

double sigma(double x)
{
    if (x>=0)
        return 1.0/(1.0+exp(-x));
    return 1.0 - 1.0/(1.0+exp(x));
}